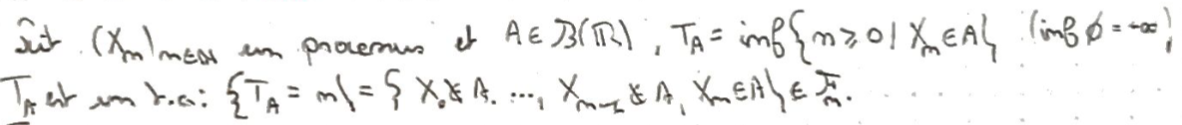Temps d'arrêt \(T\)
Variable aléatoire à valeur dans \(\overline {\Bbb N}\) telle que $$\forall n\in{\Bbb N},\qquad \{T=n\}\in{\mathcal F}_n$$pour un certaine
Filtration \(({\mathcal F}_n)_{n\in\Bbb N}\) donnée.
- la condition est équivalente à \(\forall n\in{\Bbb N},\{T\leqslant n\}\in{\mathcal F}_n\)
- si \(S\) et \(T\) sont des temps d'arrêt, alors \(S\land T\) et \(S\lor T\) sont des temps d'arrêt
Questions de cours
START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple de temps d'arrêt trivial.
Verso:
Bonus:
Carte inversée ?:
END
START
Ω Basique (+inversé optionnel)
Recto: Donner un exemple de temps d'arrêt pour un
Processus discret.
Verso:
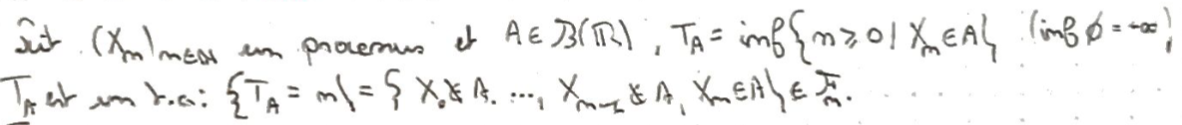
Bonus:
Carte inversée ?:
END
Exercices